🗨 개인적인 공부 기록용으로 정리한 내용입니다. 잘못된 내용에 대한 피드백은 언제나 감사합니다 :)
⭐ 스택은 마지막에 들어간 데이터가 가장 먼저 나오는 후입선출(LIFO) 구조의 자료구조이다.
📌 스택의 정의
스택은 후입선출(LIFO: Last In, First Out) 구조의 선형 자료구조이다.
즉, 가장 마지막에 추가된 요소가 가장 먼저 제거되는 방식이다.
(가장 먼저 들어온 데이터가 가장 먼저 처리되는 `큐(Queue)`와 반대되는 개념이다.)
스택은 물건을 쌓는 방식과 비슷하여 요소를 넣고(push) 빼는(pop) 작업이 맨 위에서만 일어난다.
스택의 중간에서는 요소를 삭제할 수 없다.
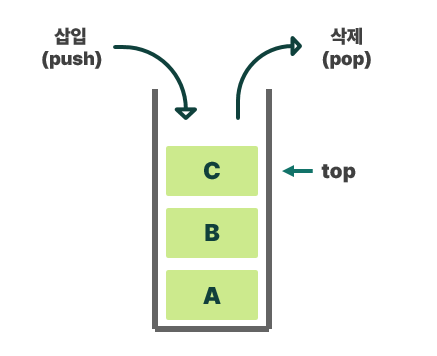
스택의 주요 연산은 다음과 같다.
- `Push`: 스택의 맨 위에 새로운 요소를 추가한다.
- `Pop`: 스택의 맨 위에 있는 요소를 제거한다.
- `isEmpty`: 스택이 비었다면 1을, 그렇지 않다면 0을 반환한다.
- `Top` or `Peek`: 스택의 맨 위에 있는 요소를 반환한다.
- (C++은 `top()`, C#은 `peek()`)
📌 스택의 장점
- 구현이 간단하다.
- 삽입(push)과 제거(pop) 연산 속도가 빠르다.
- 데이터가 스택의 맨 위에서만 추가되거나 제거되기 때문에, 위치를 찾기 위한 추가적인 탐색이 필요하지 않다.
- ⏱ 시간 복잡도: $\mathbf{O(1)}$
- 후입선출(LIFO) 방식에 최적화되어 있다.
- 예를 들어, 마지막으로 추가된 요소가 가장 먼저 필요하거나 마지막 작업부터 순차적으로 처리가 필요한 상황에서 효율적으로 쓰인다.
- 대표적으로 `되돌리기(Undo)` 기능에 사용된다.
📌 스택의 단점
- 중간 데이터에 직접 접근하거나 수정하는 것이 어렵다.
- 스택의 특정 위치에 접근하려면 맨 위 요소부터 순서대로 제거해야 한다.
- 크기가 고정된 스택인 경우, 메모리 공간의 제한이 있다. 할당된 크기를 넘는 데이터를 저장할 수 없다.
- 고정된 크기의 스택에서 제한된 공간을 초과해 데이터를 추가하려고 하면, `오버플로우(Overflow)` 에러가 발생한다.
- 이를 보완하려면, 동적 배열로 구현하거나 연결 리스트 방식으로 구현해야 한다.
📌 스택의 사용
스택은 구현이 쉬운 만큼 컴퓨터에서 아주 다양하게 응용되는 중요한 자료구조이다.
🔖 1) 함수 호출 관리(Call Stack)
프로그램이 실행될 때, 각 함수 호출마다 함수의 `지역변수`와 `반환 주소` 등을 메모리 스택에 저장한다. 함수가 종료되면 해당 함수의 정보를 제거하여 이전 함수로 돌아가도록 하는데, 이를 `콜 스택(Call Stack)`이라고 한다.
🔖 2) 재귀 함수의 처리
재귀 함수는 스택을 이용해 호출된 순서대로 데이터를 저장하고 관리한다.
재귀 호출을 통해 내려가면서 데이터를 스택에 쌓아두고, 반환 시 쌓아둔 데이터를 상단에서부터 하나씩 사용해 나간다.
🔖 3) 괄호 짝 맞추기 및 오류 검사
스택은 프로그래밍에서 괄호의 짝을 맞추는 작업에서 유용하게 사용된다.
프로그램에서 여러 가지 종류의 괄호들이 사용되는데, 우리는 이 괄호들이 항상 쌍이 되게끔 사용해야만 한다.
괄호의 종류는 `[대괄호]`, `{중괄호}`, `(소괄호)` 등이 있다.
이들이 올바르게 사용되었는지 검사하는 방법은 아래의 과정을 따른다.
- 왼쪽 괄호를 만나면 스택에 삽입한다.
- 오른쪽 괄호를 만나면 스택에서 맨 위의 괄호를 꺼낸 후 오른쪽 괄호와 짝이 맞는지 검사한다.
이와 같이, 중첩된 괄호를 만나면 열린 괄호를 스택에 추가하고, 같은 종류의 닫힌 괄호를 만났을 때 스택에서 요소를 제거하는 방식으로 올바른 괄호 순서를 확인할 수 있다.
괄호뿐만 아니라, 태그(Tag)나 따옴표 검사등에서도 활용된다.
🔖 4) 문자열 뒤집기
문자열을 뒤집는 작업에 스택을 사용하면 쉽게 해결할 수 있다.
방법은 정말 간단하다.
문자열의 각 문자를 스택에 삽입한 후, 하나씩 꺼내면서 새로운 문자열을 만들면 원래 문자열이 뒤집힌 상태가 된다.
🔖 5) Undo / Redo 기능
작업을 추적하는 기능인 `Undo` / `Redo` 기능에서도 스택이 사용된다.
사용자의 작업을 스택에 저장해 두고, 우리가 흔히 사용하는 `ctrl + z` 같이 작업을 취소할 때, 가장 최근 작업(스택의 가장 윗 데이터)을 꺼내 실행을 되돌린다.
🔖 6) 알고리즘과 데이터 처리 (DFS, 후위 표기법 계산)
그래프나 트리의 깊이 우선 탐색(DFS) 알고리즘에서 스택을 활용한다. 현재 노드를 스택에 저장하고 인접 노드를 방문하면서 탐색을 진행하며, 더 이상 방문할 인접 노드가 없으면 스택에서 제거하며 이전 노드로 돌아간다.
수식을 표기할 때, 인간은 주로 중위표기법(infix)을 사용하지만 컴파일러는 주로 후위표기법(postfix)을 사용한다.
따라서 프로그래머가 중위표기법으로 작성하면 컴파일러는 이것을 후위표기법으로 변환한 후에 계산하는데 이때, 표기법을 전환하는 과정에 스택을 이용한다.
예로, 중위 표기법을 후위 표기법으로 변환하는 과정을 간단하게 정리하면 아래와 같다.
- 피연산자(숫자나 변수)는 순서대로 출력한다.
- 연산자는 스택에 쌓는다. 스택에 있는 연산자들은 우선순위에 따라 유지된다.
- 왼쪽 괄호`(` 가 나오면 무조건 스택에 넣고, 오른쪽 괄호`)`가 나오면 왼쪽 괄호`(`가 나올 때까지 스택의 연산자를 꺼내서 출력한다.
- 모든 수식을 처리한 후, 스택에 남은 연산자를 순서대로 꺼내서 출력한다.
위 과정을 따르면, 중위 표기식 `A + (B * C)` 는 후위 표기식 `A B C * +`로 변환된다.
'💾 Computer Science > Algorithm' 카테고리의 다른 글
| [Data Structure] 자료구조 - 리스트(List), 배열 리스트(Array List), 연결 리스트(Linked List) (0) | 2024.09.12 |
|---|---|
| [Data Structure] 자료구조 - 배열(Array) (0) | 2024.09.12 |
| [Data Structure] 자료구조(Data Structure)란? (선형&비선형 자료구조) (0) | 2024.09.06 |