🗨 개인적인 공부 목적으로 정리한 내용입니다. 잘못된 내용에 대한 피드백은 언제나 감사합니다 :)
⭐ 에라토스테네스의 체는 작은 수부터 시작하여 소수의 배수를 지워나가는 방식으로 소수를 찾는 고효율적인 알고리즘이다.
📌 에라토스테네스의 체 (Sieve of Eratosthenes)
고대 그리스의 수학자인 에라토스테네스가 발견한 소수를 찾는 가장 빠르고 쉬운 방법이다.
⏱ $\mathbf{O(n\;log\;log\;n)}$ 의 시간 복잡도를 가진다.
아래 동작 원리 부분을 보면 알겠지만, 지워진 부분도 차례가 되면 불필요하게 탐색하기 때문에 이를 보완한 방법도 존재한다.
이는 기존의 에라토스테네스의 체를 개선한 "선형 에라토스테네스의 체"로, 시간 복잡도를 $O(n)$으로 줄인 알고리즘이다.
❗ 다만, "n이 소수인가?"와 같은 상황이 아닌, "특정 범위 내의 소수"를 판정하는 데에만 효율적이다.
n이라는 하나의 수에 대한 소수를 판정하는 방법은 에라토스테네스의 체보다 빠른 방법들이 많다!

📌 에라토스테네스의 체: 동작 원리
❕ 0과 1은 소수가 아니므로 2부터 시작한다.
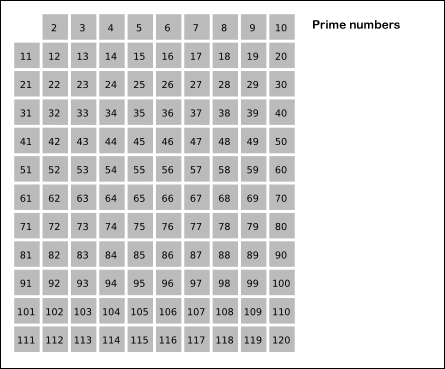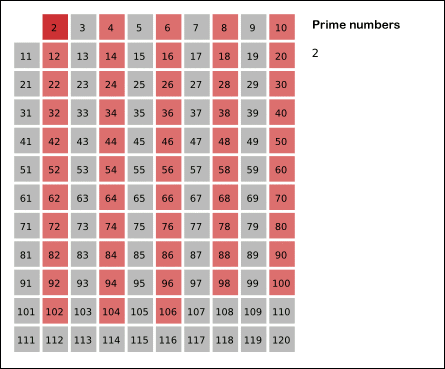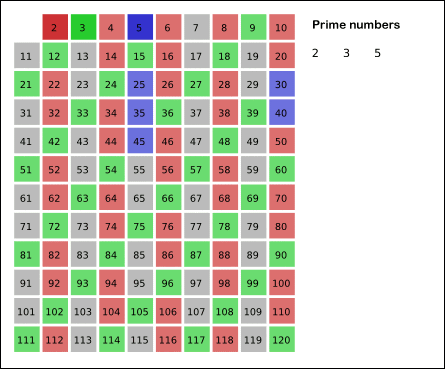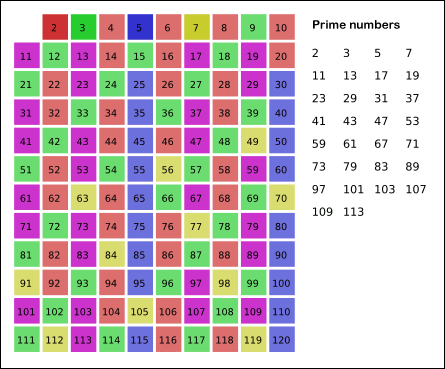
2부터 n까지의 범위에서 소수를 찾아내는 방법은 아래와 같다.
- 2부터 n까지의 숫자를 나열한다.
- 가장 작은 숫자 2를 소수로 선택하고, 2의 배수들을 모두 제거한다. (현재까지 찾은 소수 : 2)
- 다음으로 남아있는 가장 작은 숫자 3을 소수로 선택하고, 3의 배수들을 모두 제거한다. (현재까지 찾은 소수 : 2, 3)
- 4는 위의 과정 2에서 제거되었으므로 패스
- 다음으로 남아있는 가장 작은 숫자 5를 소수로 선택하고, 5의 배수들을 모두 제거한다. (현재까지 찾은 소수 : 2, 3, 5)
- 위의 과정들을 반복하면 n까지의 모든 소수를 구할 수 있다.
🔎 n의 제곱근까지 위의 과정을 반복하면 된다.
n의 제곱근보다 작은 수의 배수만 제거해도 n보다 작으면서 소수가 아닌 수들은 전부 지워진다.
📌 에라토스테네스의 체: 코드 구현
에라토스테네스의 체를 C++코드로 구현하면 아래와 같다.
#include <iostream>
#include <vector>
using namespace std;
void Eratos (int n) {
/* n까지의 소수를 구하기 위한 리스트 생성 (true: 소수, false: 소수 아님) */
vector<bool> isPrime(n + 1, true);
/* 0과 1은 소수가 아니므로 false로 설정 */
isPrime[0] = isPrime[1] = false;
/* 2부터 시작하여 n의 제곱근까지 반복 */
for (int p = 2; p * p <= n; p++) {
/* 만약 p가 소수이면 */
if (isPrime[p]) {
/* p의 배수들을 모두 false로 바꿈 */
for (int i = p * p; i <= n; i += p) {
isPrime[i] = false;
}
}
}
/* 소수 출력 */
cout << "2부터 n까지의 소수: ";
for (int p = 2; p <= n; p++) {
if (isPrime[p]) {
cout << p << ' ';
}
}
}
int main() {
int n;
cout << "입력: ";
cin >> n;
Eratos(n);
}
입출력 결과
입력: 120
2부터 n까지의 소수: 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113
참고
에라토스테네스의 체 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 에라토스테네스의 체 수학에서 에라토스테네스의 체는 소수를 찾는 빠르고 쉬운 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다. 2부터 소수를
ko.wikipedia.org
'💾 Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 선형 에라토스테네스의 체(선형 체, Linear Sieve) : O(n)으로 소수 구하기! (1) | 2024.10.16 |
|---|---|
| [Data Structure] 자료구조 - 리스트(List), 배열 리스트(Array List), 연결 리스트(Linked List) (0) | 2024.09.12 |
| [Data Structure] 자료구조 - 스택(Stack) (0) | 2024.09.12 |
🗨 개인적인 공부 목적으로 정리한 내용입니다. 잘못된 내용에 대한 피드백은 언제나 감사합니다 :)
⭐ 에라토스테네스의 체는 작은 수부터 시작하여 소수의 배수를 지워나가는 방식으로 소수를 찾는 고효율적인 알고리즘이다.
📌 에라토스테네스의 체 (Sieve of Eratosthenes)
고대 그리스의 수학자인 에라토스테네스가 발견한 소수를 찾는 가장 빠르고 쉬운 방법이다.
⏱ $\mathbf{O(n\;log\;log\;n)}$ 의 시간 복잡도를 가진다.
아래 동작 원리 부분을 보면 알겠지만, 지워진 부분도 차례가 되면 불필요하게 탐색하기 때문에 이를 보완한 방법도 존재한다.
이는 기존의 에라토스테네스의 체를 개선한 "선형 에라토스테네스의 체"로, 시간 복잡도를 $O(n)$으로 줄인 알고리즘이다.
❗ 다만, "n이 소수인가?"와 같은 상황이 아닌, "특정 범위 내의 소수"를 판정하는 데에만 효율적이다.
n이라는 하나의 수에 대한 소수를 판정하는 방법은 에라토스테네스의 체보다 빠른 방법들이 많다!

📌 에라토스테네스의 체: 동작 원리
❕ 0과 1은 소수가 아니므로 2부터 시작한다.

2부터 n까지의 범위에서 소수를 찾아내는 방법은 아래와 같다.
- 2부터 n까지의 숫자를 나열한다.
- 가장 작은 숫자 2를 소수로 선택하고, 2의 배수들을 모두 제거한다. (현재까지 찾은 소수 : 2)
- 다음으로 남아있는 가장 작은 숫자 3을 소수로 선택하고, 3의 배수들을 모두 제거한다. (현재까지 찾은 소수 : 2, 3)
- 4는 위의 과정 2에서 제거되었으므로 패스
- 다음으로 남아있는 가장 작은 숫자 5를 소수로 선택하고, 5의 배수들을 모두 제거한다. (현재까지 찾은 소수 : 2, 3, 5)
- 위의 과정들을 반복하면 n까지의 모든 소수를 구할 수 있다.
🔎 n의 제곱근까지 위의 과정을 반복하면 된다.
n의 제곱근보다 작은 수의 배수만 제거해도 n보다 작으면서 소수가 아닌 수들은 전부 지워진다.
📌 에라토스테네스의 체: 코드 구현
에라토스테네스의 체를 C++코드로 구현하면 아래와 같다.
#include <iostream> #include <vector> using namespace std; void Eratos (int n) { /* n까지의 소수를 구하기 위한 리스트 생성 (true: 소수, false: 소수 아님) */ vector<bool> isPrime(n + 1, true); /* 0과 1은 소수가 아니므로 false로 설정 */ isPrime[0] = isPrime[1] = false; /* 2부터 시작하여 n의 제곱근까지 반복 */ for (int p = 2; p * p <= n; p++) { /* 만약 p가 소수이면 */ if (isPrime[p]) { /* p의 배수들을 모두 false로 바꿈 */ for (int i = p * p; i <= n; i += p) { isPrime[i] = false; } } } /* 소수 출력 */ cout << "2부터 n까지의 소수: "; for (int p = 2; p <= n; p++) { if (isPrime[p]) { cout << p << ' '; } } } int main() { int n; cout << "입력: "; cin >> n; Eratos(n); }
입출력 결과
입력: 120 2부터 n까지의 소수: 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113
참고
에라토스테네스의 체 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 에라토스테네스의 체 수학에서 에라토스테네스의 체는 소수를 찾는 빠르고 쉬운 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다. 2부터 소수를
ko.wikipedia.org
'💾 Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 선형 에라토스테네스의 체(선형 체, Linear Sieve) : O(n)으로 소수 구하기! (1) | 2024.10.16 |
|---|---|
| [Data Structure] 자료구조 - 리스트(List), 배열 리스트(Array List), 연결 리스트(Linked List) (0) | 2024.09.12 |
| [Data Structure] 자료구조 - 스택(Stack) (0) | 2024.09.12 |
