🗨 개인적인 공부 목적으로 정리한 내용입니다. 잘못된 내용에 대한 피드백은 언제나 감사합니다 :)
⭐ Longest Common Subsequence(LCS) 알고리즘은 두 문자열에서 순서를 유지하면서 공통으로 나타나는 가장 긴 부분 수열을 동적 계획법(Dynamic Programming)으로 찾아내는 알고리즘이다.
📌 Longest Common Subsequence (LCS) vs Longest Common Substring
Longest Common Subsequence(최장 공통 부분 수열, LCS)는 두 개의 문자열이나 수열 사이에서 순서를 유지하면서 연속하지 않아도 되는 공통된 부분을 말한다.
이 알고리즘과 비슷하면서 다른 Longest Common Substring(최장 공통 문자열)도 있으니 차이를 알아두자. 최장 공통 문자열은 연속된 공통 부분을 찾는 알고리즘이다. 여기서 '연속된'은 문자가 붙어있어야 한다는 의미이다.
두 알고리즘 모두 약자로 LCS이지만, 이 글의 LCS는 Longest Common Subsequence(최장 공통 부분 수열)을 의미한다.
LCS는 일반적으로, Longest Common Subsequence를 뜻한다.
❓ 그럼, LCS가 무엇인가?
예를 들어, 두 문자열 "ABCDEF" 와 "ACCDE" 가 있다고 하자.
- 순서를 유지하면서 연속하지 않아도 되는 공통 부분, 즉 Longest Common Subsequence는 "ACDE" 를 가리킨다.
- "ABCDEF" "ACCDE"
- Longest Common Substring은 순서를 유지하면서 연속하는 공통 부분이므로, "DE" 가 된다.
- "ABCDEF" "ACCDE"
LCS는 유일하지 않다. 즉, 여러 개가 존재할 수 있다.
예를 들어, "ABCD" 와 "ACB" 에서 LCS를 찾으면, "AC" "AB"가 해당된다.
❓ LCS 알고리즘은 어디에 사용되는가?
대표적으로, diff(파일 비교 유틸리티), 생물정보학에서는 DNA 서열 분석에 사용되는 등 응용되는 분야가 다양하다.
알고리즘 문제에서도 Dynamic Programming과 관련하여 빈번하게 등장한다.
⏱ 이 알고리즘은 두 문자열의 길이에 비례하여 작동하므로, $\mathbf{O(m * n)}$의 시간 복잡도를 가진다.
📌 LCS (최장 공통 부분 수열) 알고리즘: 동작 원리
LCS 알고리즘은 동적 계획법(DP)을 사용하여, 작은 문제를 해결하면서 최종 답을 구하는 방식이다.
- 두 문자열의 길이를 각각 m, n이라고 할 때, 크기가 (m+1) * (n+1) 인 2차원 배열 dp을 이용한다.
- dp[i][j]는 str1의 처음 i개 문자와 str2의 처음 j개 문자 사이의 LCS 길이를 저장한다.
- 문자를 비교하며 두 문자가 같으면 이전까지의 LCS 길이에 1을 더하고, 문자가 다르면 현재 위치에서 하나의 문자를 제외했을 때의 최댓값을 가져오는 식으로 진행된다.
🧩 동작 원리는 아래와 같다.
1. 두 문자열 str1과 str2를 입력받는다.
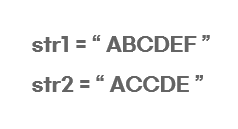
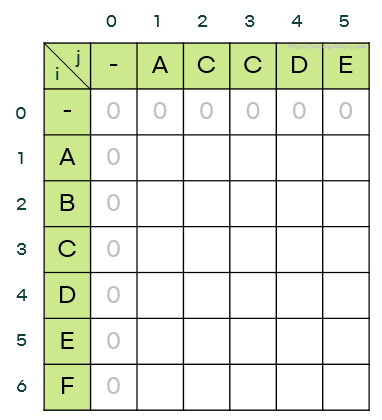
2. 두 문자열의 길이가 각각 6, 5이므로, 크기가 $(6+1) * (5+1)$ 인 2차원 배열 dp을 생성한다.
- 처음에는 dp[0][j] 와 dp[i][0]은 0으로 초기화한다. (빈 문자열과의 비교는 LCS 길이가 0이기 때문이다.)
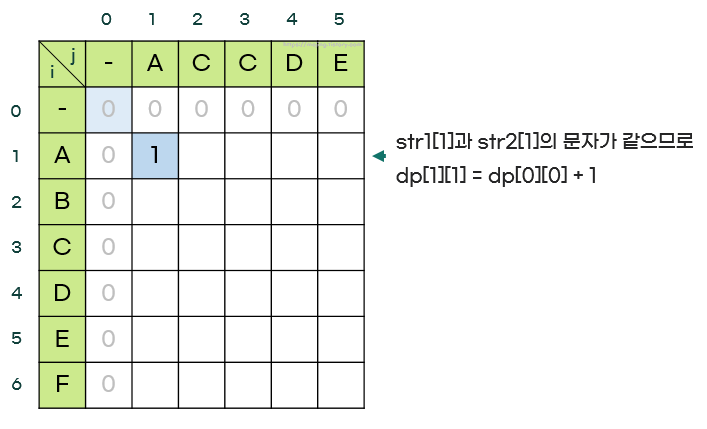
3. str1의 첫 문자인 'A'와 str2의 문자들을 비교하며 아래 조건에 따라 dp를 채워나간다.
- 문자가 같을 때:
- 만약, str1[i-1] == str2[j-1] 라면, dp[i][j] = dp[i-1][j-1] + 1
- 즉, 문자가 같으면 이전까지의 LCS 길이에 1을 더한다.
- 문자가 다를 때:
- 만약, str1[i-1] != str2[j-1] 라면, dp[i][j] = max(dp[i-1][j], dp[i][j-1])
- 즉, 문자가 다르면 현재 위치에서 하나의 문자열을 제외했을 때의 최댓값을 가져온다.
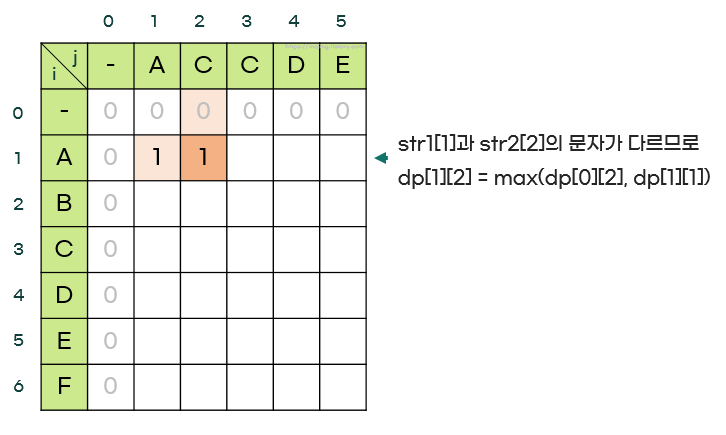
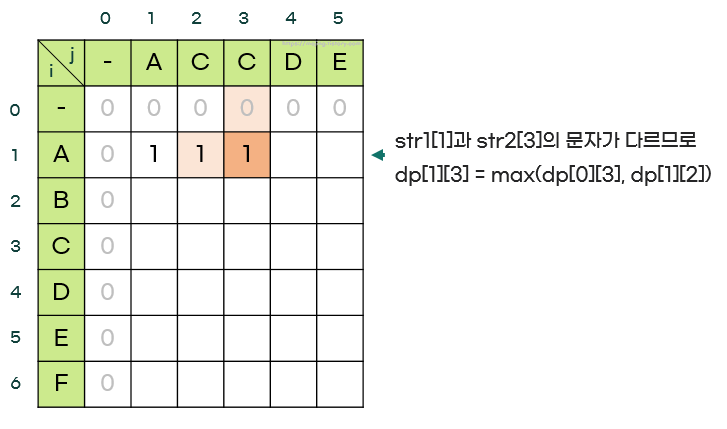
- 1행이 전부 채워진 모습은 다음과 같다.
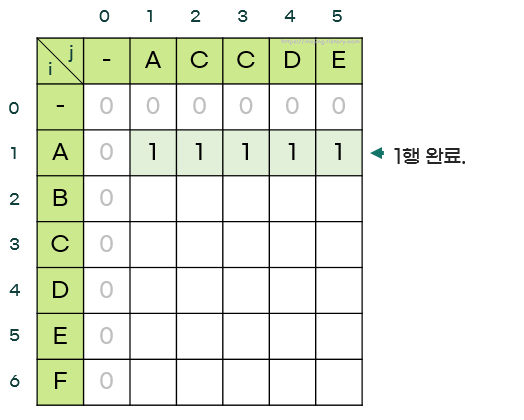
4. 같은 방법으로 str1의 두 번째 문자인 'B'와 str2의 문자들을 비교한다.
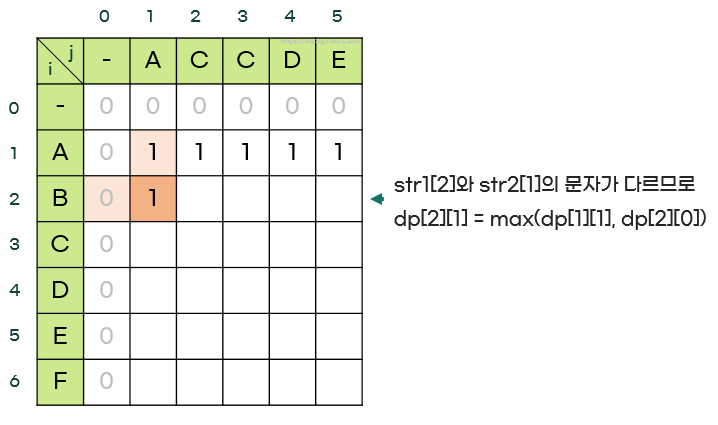
- 2행을 전부 채운다.
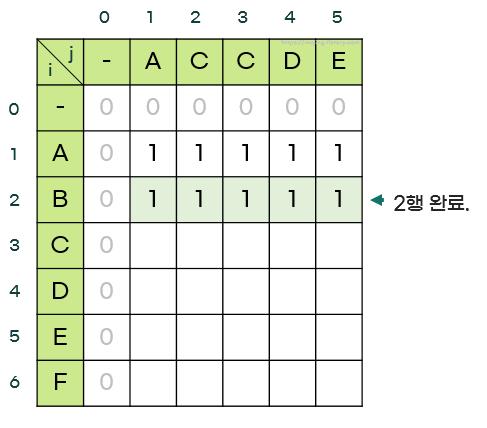
5. 3행부터 dp 배열을 모두 채우면 아래와 같은 모습이다.
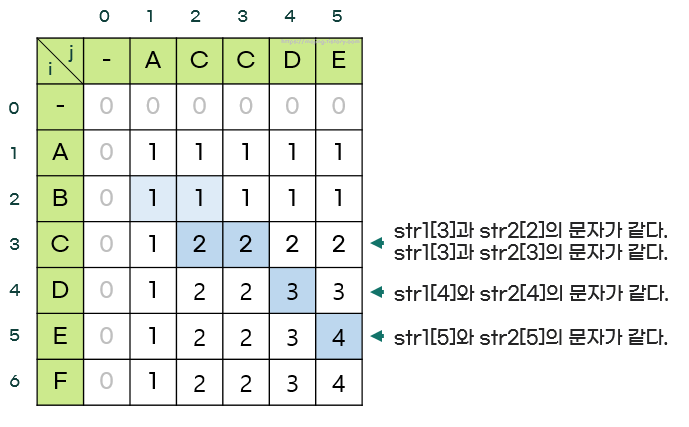
6. 배열이 전부 채워지면, 마지막 값인 dp[6][5] (= dp[m][n]) = 4가 최장 공통 부분 수열(LCS)의 길이를 나타낸다.
🔖 LCS 역추적
아래 설명은 LCS 자체를 구하는 과정이다.
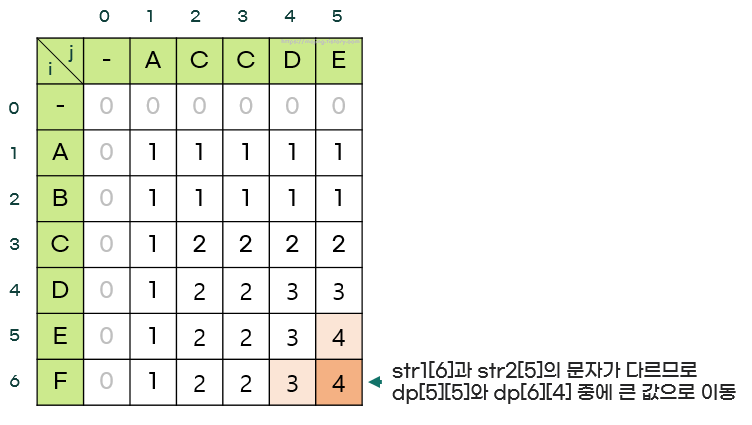
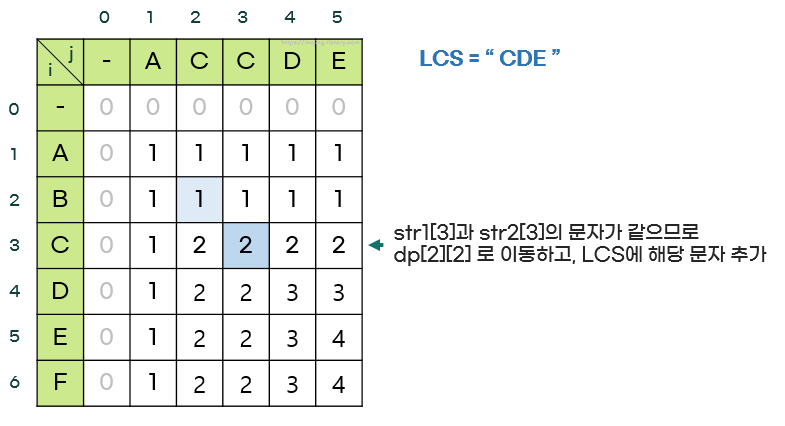
길이가 아닌, LCS 자체를 구하기 위해서는 위의 dp 테이블을 역추적한다.
- dp[i][j]에서 시작해서 dp[i-1][j-1]로 이동할 때는 두 문자가 같다는 의미이므로 그 문자를 LCS에 추가한다.
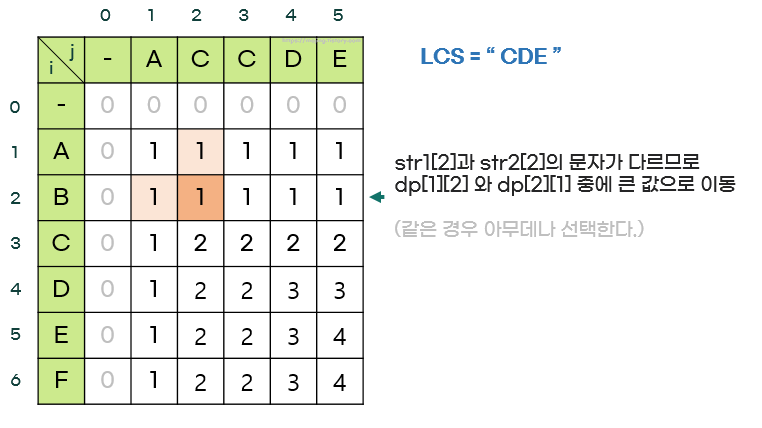
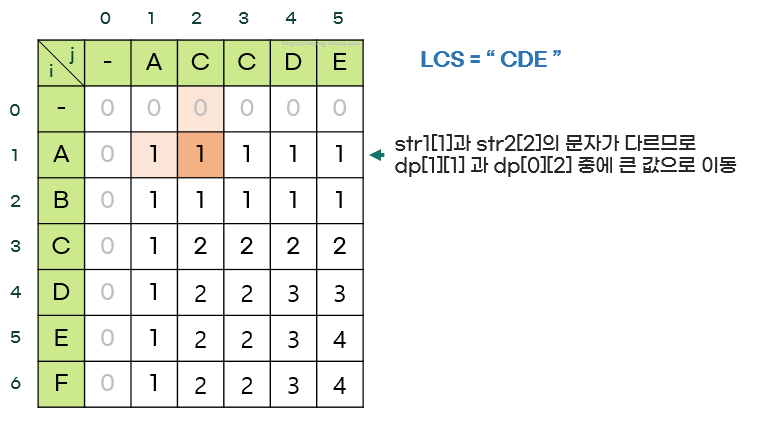
- 문자가 다를 때는 dp[i-1][j]와 dp[i][j-1] 중 더 큰 값을 선택해 이동한다.
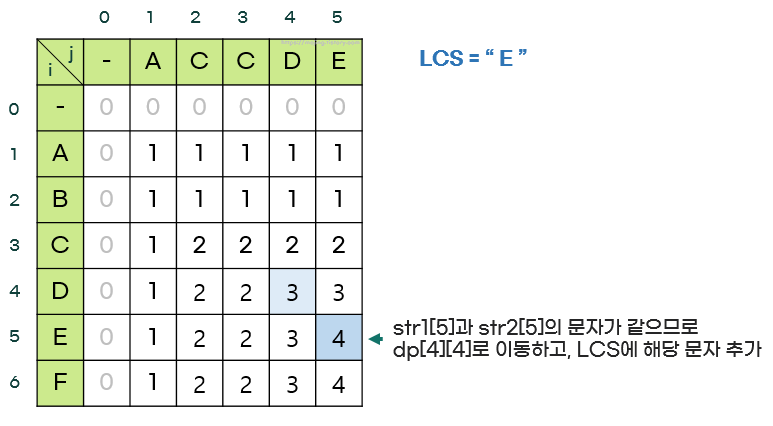
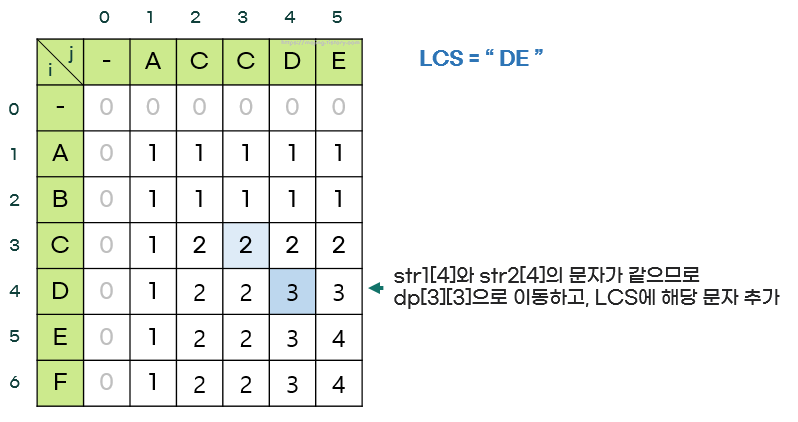
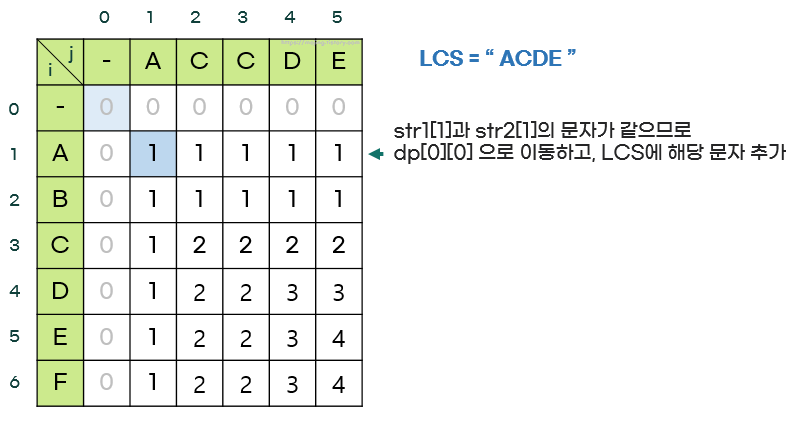
마지막으로 i와 j가 0이므로 종료한다.
이렇게 역추적으로 LCS 자체를 구할 수 있다.
📌 LCS (최장 공통 부분 수열) 알고리즘: 코드 구현
LCS 알고리즘을 C++코드로 구현하면 아래와 같다.
#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
using namespace std;
int main() {
string str1, str2;
cout << "입력: ";
cin >> str1 >> str2;
int m = str1.size();
int n = str2.size();
/* m x n 크기의 2차원 DP 배열 선언 */
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
/* DP 테이블 채우기 */
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (str1[i - 1] == str2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
}
}
/* LCS 길이 출력 */
cout << "LCS의 길이: " << dp[m][n] << "\n";
/* LCS 역추적 */
string lcs = "";
int i = m, j = n;
while (i > 0 && j > 0) {
if (str1[i - 1] == str2[j - 1]) {
lcs = str1[i - 1] + lcs;
i--; j--;
}
else if (dp[i - 1][j] > dp[i][j - 1]) {
i--;
}
else {
j--;
}
}
/* LCS 문자열 출력 */
cout << "LCS 문자열: " << lcs << "\n\n";
/* DP 테이블 출력 */
cout << "DP[][]: " << "\n";
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
cout << dp[i][j] << ' ';
}
cout << "\n";
}
}
입출력 결과
입력: ABCDEF ACCDE
LCS의 길이: 4
LCS 문자열: ACDE
DP[][]:
0 0 0 0 0 0
0 1 1 1 1 1
0 1 1 1 1 1
0 1 2 2 2 2
0 1 2 2 3 3
0 1 2 2 3 4
0 1 2 2 3 4
참고
최장 공통 부분 수열 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 최장 공통 부분수열 문제는 LCS라고도 불린다. 이는 주어진 여러 개의 수열 모두의 부분수열이 되는 수열들 중에 가장 긴 것을 찾는 문제다.(종종 단 두 개중 하
ko.wikipedia.org
[알고리즘] 그림으로 알아보는 LCS 알고리즘 - Longest Common Substring와 Longest Common Subsequence
[알고리즘] 그림으로 알아보는 LCS 알고리즘 - Longest Common Substring와 Longest Common Subsequence
LCS는 주로 최장 공통 부분수열(Longest Common Subsequence)을 말합니다만, 최장 공통 문자열(Longest Common Substring)을 말하기도 합니다.
velog.io
'💾 Computer Science > Algorithm' 카테고리의 다른 글
| [Data Structure] 자료구조 - 큐(Queue), 원형 큐, 우선순위 큐, 데크 (0) | 2024.11.04 |
|---|---|
| [Algorithm] 선형 에라토스테네스의 체(선형 체, Linear Sieve) : O(n)으로 소수 구하기! (1) | 2024.10.16 |
| [Algorithm] 에라토스테네스의 체(Sieve of Eratosthenes) : 소수를 구하는 고효율 알고리즘 (0) | 2024.10.15 |
🗨 개인적인 공부 목적으로 정리한 내용입니다. 잘못된 내용에 대한 피드백은 언제나 감사합니다 :)
⭐ Longest Common Subsequence(LCS) 알고리즘은 두 문자열에서 순서를 유지하면서 공통으로 나타나는 가장 긴 부분 수열을 동적 계획법(Dynamic Programming)으로 찾아내는 알고리즘이다.
📌 Longest Common Subsequence (LCS) vs Longest Common Substring
Longest Common Subsequence(최장 공통 부분 수열, LCS)는 두 개의 문자열이나 수열 사이에서 순서를 유지하면서 연속하지 않아도 되는 공통된 부분을 말한다.
이 알고리즘과 비슷하면서 다른 Longest Common Substring(최장 공통 문자열)도 있으니 차이를 알아두자. 최장 공통 문자열은 연속된 공통 부분을 찾는 알고리즘이다. 여기서 '연속된'은 문자가 붙어있어야 한다는 의미이다.
두 알고리즘 모두 약자로 LCS이지만, 이 글의 LCS는 Longest Common Subsequence(최장 공통 부분 수열)을 의미한다.
LCS는 일반적으로, Longest Common Subsequence를 뜻한다.
❓ 그럼, LCS가 무엇인가?
예를 들어, 두 문자열 "ABCDEF" 와 "ACCDE" 가 있다고 하자.
- 순서를 유지하면서 연속하지 않아도 되는 공통 부분, 즉 Longest Common Subsequence는 "ACDE" 를 가리킨다.
- "ABCDEF" "ACCDE"
- Longest Common Substring은 순서를 유지하면서 연속하는 공통 부분이므로, "DE" 가 된다.
- "ABCDEF" "ACCDE"
LCS는 유일하지 않다. 즉, 여러 개가 존재할 수 있다.
예를 들어, "ABCD" 와 "ACB" 에서 LCS를 찾으면, "AC" "AB"가 해당된다.
❓ LCS 알고리즘은 어디에 사용되는가?
대표적으로, diff(파일 비교 유틸리티), 생물정보학에서는 DNA 서열 분석에 사용되는 등 응용되는 분야가 다양하다.
알고리즘 문제에서도 Dynamic Programming과 관련하여 빈번하게 등장한다.
⏱ 이 알고리즘은 두 문자열의 길이에 비례하여 작동하므로, $\mathbf{O(m * n)}$의 시간 복잡도를 가진다.
📌 LCS (최장 공통 부분 수열) 알고리즘: 동작 원리
LCS 알고리즘은 동적 계획법(DP)을 사용하여, 작은 문제를 해결하면서 최종 답을 구하는 방식이다.
- 두 문자열의 길이를 각각 m, n이라고 할 때, 크기가 (m+1) * (n+1) 인 2차원 배열 dp을 이용한다.
- dp[i][j]는 str1의 처음 i개 문자와 str2의 처음 j개 문자 사이의 LCS 길이를 저장한다.
- 문자를 비교하며 두 문자가 같으면 이전까지의 LCS 길이에 1을 더하고, 문자가 다르면 현재 위치에서 하나의 문자를 제외했을 때의 최댓값을 가져오는 식으로 진행된다.
🧩 동작 원리는 아래와 같다.
1. 두 문자열 str1과 str2를 입력받는다.
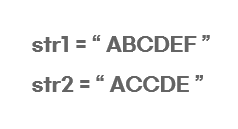
2. 두 문자열의 길이가 각각 6, 5이므로, 크기가 $(6+1) * (5+1)$ 인 2차원 배열 dp을 생성한다.
- 처음에는 dp[0][j] 와 dp[i][0]은 0으로 초기화한다. (빈 문자열과의 비교는 LCS 길이가 0이기 때문이다.)

3. str1의 첫 문자인 'A'와 str2의 문자들을 비교하며 아래 조건에 따라 dp를 채워나간다.
- 문자가 같을 때:
- 만약, str1[i-1] == str2[j-1] 라면, dp[i][j] = dp[i-1][j-1] + 1
- 즉, 문자가 같으면 이전까지의 LCS 길이에 1을 더한다.
- 문자가 다를 때:
- 만약, str1[i-1] != str2[j-1] 라면, dp[i][j] = max(dp[i-1][j], dp[i][j-1])
- 즉, 문자가 다르면 현재 위치에서 하나의 문자열을 제외했을 때의 최댓값을 가져온다.



- 1행이 전부 채워진 모습은 다음과 같다.

4. 같은 방법으로 str1의 두 번째 문자인 'B'와 str2의 문자들을 비교한다.

- 2행을 전부 채운다.

5. 3행부터 dp 배열을 모두 채우면 아래와 같은 모습이다.

6. 배열이 전부 채워지면, 마지막 값인 dp[6][5] (= dp[m][n]) = 4가 최장 공통 부분 수열(LCS)의 길이를 나타낸다.
🔖 LCS 역추적
아래 설명은 LCS 자체를 구하는 과정이다.
길이가 아닌, LCS 자체를 구하기 위해서는 위의 dp 테이블을 역추적한다.
- dp[i][j]에서 시작해서 dp[i-1][j-1]로 이동할 때는 두 문자가 같다는 의미이므로 그 문자를 LCS에 추가한다.
- 문자가 다를 때는 dp[i-1][j]와 dp[i][j-1] 중 더 큰 값을 선택해 이동한다.







마지막으로 i와 j가 0이므로 종료한다.
이렇게 역추적으로 LCS 자체를 구할 수 있다.
📌 LCS (최장 공통 부분 수열) 알고리즘: 코드 구현
LCS 알고리즘을 C++코드로 구현하면 아래와 같다.
#include <iostream> #include <algorithm> #include <string> #include <vector> using namespace std; int main() { string str1, str2; cout << "입력: "; cin >> str1 >> str2; int m = str1.size(); int n = str2.size(); /* m x n 크기의 2차원 DP 배열 선언 */ vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0)); /* DP 테이블 채우기 */ for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { if (str1[i - 1] == str2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1; else dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]); } } /* LCS 길이 출력 */ cout << "LCS의 길이: " << dp[m][n] << "\n"; /* LCS 역추적 */ string lcs = ""; int i = m, j = n; while (i > 0 && j > 0) { if (str1[i - 1] == str2[j - 1]) { lcs = str1[i - 1] + lcs; i--; j--; } else if (dp[i - 1][j] > dp[i][j - 1]) { i--; } else { j--; } } /* LCS 문자열 출력 */ cout << "LCS 문자열: " << lcs << "\n\n"; /* DP 테이블 출력 */ cout << "DP[][]: " << "\n"; for (int i = 0; i <= m; i++) { for (int j = 0; j <= n; j++) { cout << dp[i][j] << ' '; } cout << "\n"; } }
입출력 결과
입력: ABCDEF ACCDE LCS의 길이: 4 LCS 문자열: ACDE DP[][]: 0 0 0 0 0 0 0 1 1 1 1 1 0 1 1 1 1 1 0 1 2 2 2 2 0 1 2 2 3 3 0 1 2 2 3 4 0 1 2 2 3 4
참고
최장 공통 부분 수열 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 최장 공통 부분수열 문제는 LCS라고도 불린다. 이는 주어진 여러 개의 수열 모두의 부분수열이 되는 수열들 중에 가장 긴 것을 찾는 문제다.(종종 단 두 개중 하
ko.wikipedia.org
[알고리즘] 그림으로 알아보는 LCS 알고리즘 - Longest Common Substring와 Longest Common Subsequence
[알고리즘] 그림으로 알아보는 LCS 알고리즘 - Longest Common Substring와 Longest Common Subsequence
LCS는 주로 최장 공통 부분수열(Longest Common Subsequence)을 말합니다만, 최장 공통 문자열(Longest Common Substring)을 말하기도 합니다.
velog.io
'💾 Computer Science > Algorithm' 카테고리의 다른 글
| [Data Structure] 자료구조 - 큐(Queue), 원형 큐, 우선순위 큐, 데크 (0) | 2024.11.04 |
|---|---|
| [Algorithm] 선형 에라토스테네스의 체(선형 체, Linear Sieve) : O(n)으로 소수 구하기! (1) | 2024.10.16 |
| [Algorithm] 에라토스테네스의 체(Sieve of Eratosthenes) : 소수를 구하는 고효율 알고리즘 (0) | 2024.10.15 |
