🗨 개인적인 공부 기록용으로 정리한 내용입니다. 잘못된 내용에 대한 피드백은 언제나 감사합니다 :)
⭐ 해시 테이블은 키(Key)를 해시 함수를 통해 해시 값으로 변환하고, 이를 인덱스로 사용하여 데이터를 저장하는 자료구조이다.
📌 해시 테이블의 정의
해시 테이블은 키(Key)를 특정 연산(해시 함수, Hash Function)을 통해 해시 값(Hash Value)으로 변환하고, 이를 인덱스로 사용하여 데이터를 저장하는 키-값(Key-Value) 매핑 자료구조이다.
일반적으로 해시 맵(Hash Map)이라고도 하며, 빠른 검색, 삽입, 삭제가 가능한 점이 특징이다.
키-값 구조는 "사전(Dictionary)"으로 예를 들 수 있다.
사전(Dictionary)은 단어(키, Key)와 뜻(값, Value)을 매핑하는 구조이다. 예를 들어 `"Apple"`이라는 단어로 검색을 한다면 `"사과"`라는 뜻을 얻을 수 있다.
해시 테이블은 이러한 사전의 개념을 프로그래밍에서 그대로 구현한 자료구조이다.
🔖 해시 테이블의 동작 원리
❓ "배열에 저장하면 되는데 왜 해시 테이블을 쓰는가?"
해시 테이블은 배열과는 비교할 수 없는 똑똑하고 빠른 검색 속도가 가장 큰 특징이다.
(똑똑한 방법이라고 한 이유는 컴퓨터에서는 모든 정보가 "수"로 이루어진 점을 이용해 수학적이고 효율적으로 데이터를 관리하는 방법이기 때문이다.)
예를 들어 물건을 정리할 때, 모든 물건을 한 공간에 모아둘 수도 있지만, 구역을 나눠서 "이건 A구역, 저건 B구역.." 이런 식으로 정리를 하면 나중에 찾을 때 해당 구역만 탐색을 하면 되기 때문에 효율적이다.
위의 정리 방법 중 전자는 배열, 후자는 해시 테이블의 데이터 저장 방식과 유사하다.
자세한 동작 원리는 다음과 같다.
`배열`과 `해시테이블`의 데이터 저장 및 검색 과정을 비교하였다.
- 아래의 `키-값 구조`의 데이터를 저장하려고 한다.
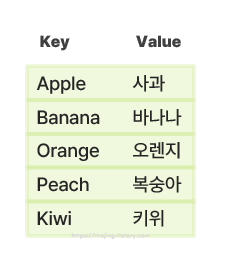
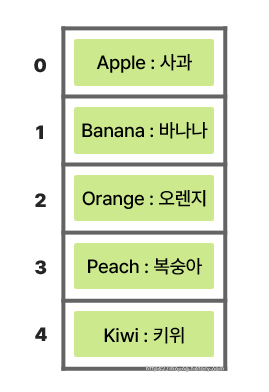
🧩 <배열: 저장>
- `배열`의 경우, 고정된 크기의 공간에 차례대로 저장된다.
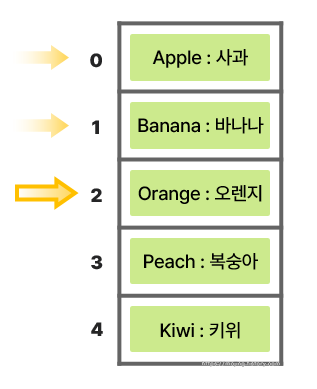
🧩 <배열: 검색>
- 여기서 `"Orange"`의 뜻을 알고 싶다고 가정하면, 배열의 0번 인덱스부터 `선형 탐색`을 한다.
- 2번 인덱스에 저장된 키(Key)가 `"Orange"`와 일치하므로 값(Value)을 불러온다.
⏱ `선형 탐색`은 $\mathbf{O(n)}$ 의 시간 복잡도를 가지므로 데이터가 많을수록 찾는 시간도 오래 걸린다.
🧩 <해시 테이블: 저장>
해시 테이블은 `키`를 `해시 함수`를 이용하여 `인덱스`로 변환하고, 해당 인덱스에 `키-값 데이터`를 저장한다.
키와 해시 함수로 실제 데이터를 저장할 주소를 반환받는 것이다.
❓ 해시 함수 (Hash Function)
해시 함수란? 주어진 데이터를 고정 길이의 불규칙한 숫자로 변환하는 함수를 가리킨다.
해시 함수의 대표적인 알고리즘으로 SHA가 있다. 🔗 SHA
아래에서 사용하는 해시 함수는 모듈로 연산(나머지 연산, mod)을 이용하였다. (글자 수 % 배열 크기)
이처럼 나머지 연산자(mod)를 사용해 키를 해시 테이블의 크기로 나눈 나머지를 해시 주소로 사용하는 방법을 `제산함수`라고 한다.
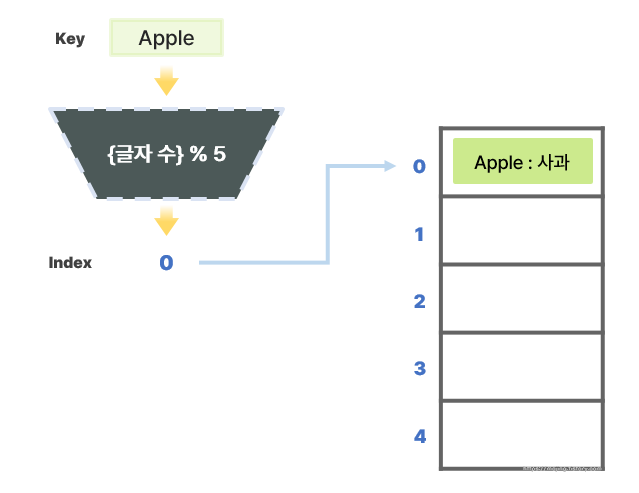
- 먼저 키(Key)인 `"Apple"`을 해시 함수를 이용해 해시 값을 추출한다.
- `"Apple"`의 글자 수는 5이므로 해시 값으로 0이 나온다. 이 0을 인덱스로 이용하여 키-값 데이터를 저장한다.
- 키(Key) `"Banana"`는 해시 함수를 이용해 변환하면 6 % 5 = 1이므로, 1번 인덱스에 데이터를 저장하게 된다.
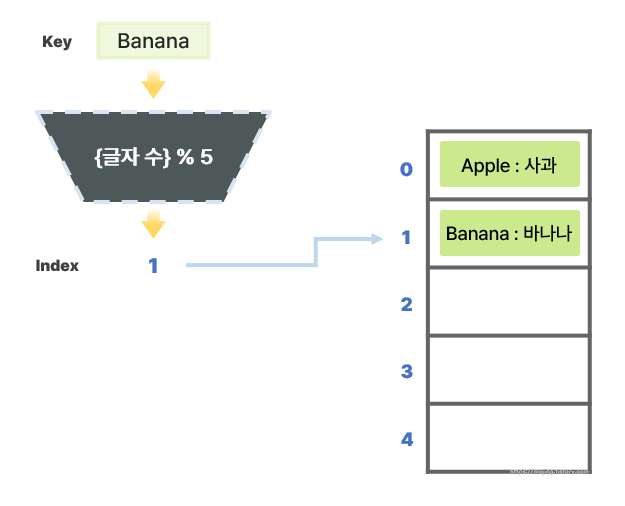
- 키(Key) `"Orange"`는 해시 함수를 이용해 변환하면 6 % 5 = 1이므로, 1번 인덱스에 데이터를 저장하게 된다.
- ❗ 그런데 이미 1번 인덱스에는 `"Banana"`의 데이터가 저장되어 있다. 이렇게 서로 다른 키(Key)가 해시 함수에 의해 저장 위치가 겹치는 것을 충돌(Collision)이라 한다.
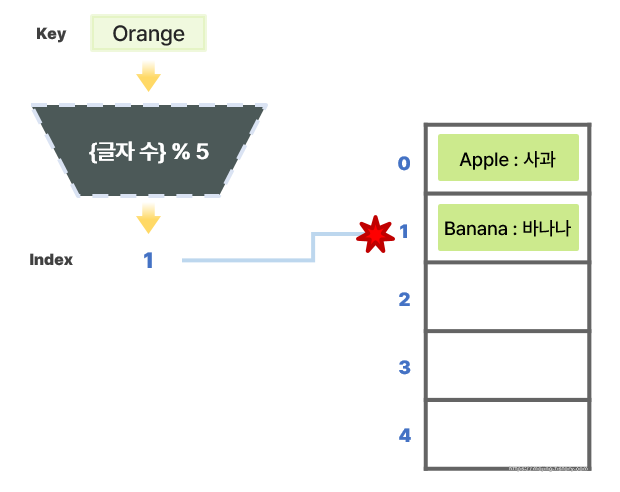
- 겹친 저장위치에 저장을 시도하면 오버플로우(Overflow)가 발생하므로, 충돌 문제 해결 방법이 필요하다.
- 대표적인 충돌 해결 방법에는 두 가지가 있다.
- `체이닝(Chaining)`: 같은 해시 값을 가지는 데이터들을 연결 리스트(Linked List) 또는 트리(Tree)를 사용하여 저장하는 방식.
- `오픈 어드레싱(Open Addressing)`: 충돌이 발생하면 다른 빈 공간을 찾아 데이터를 저장하는 방식.
- 이 중에 연결 리스트를 사용하는 체이닝 기법을 이용하면 아래와 같다.
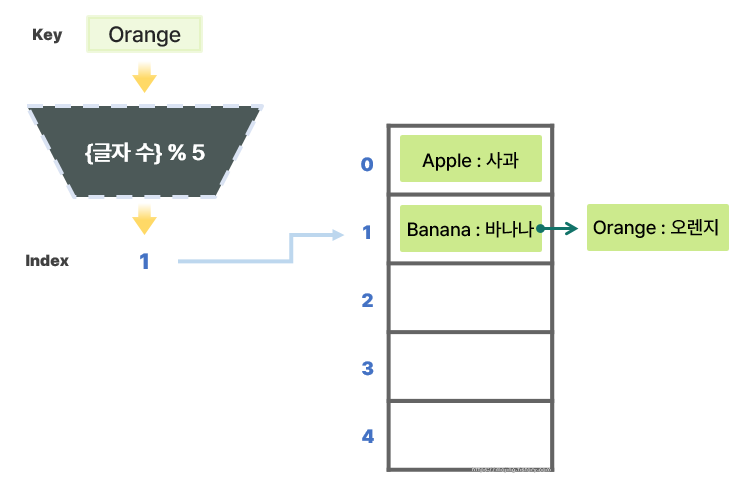
- 나머지 데이터들을 저장하면 아래와 같다.
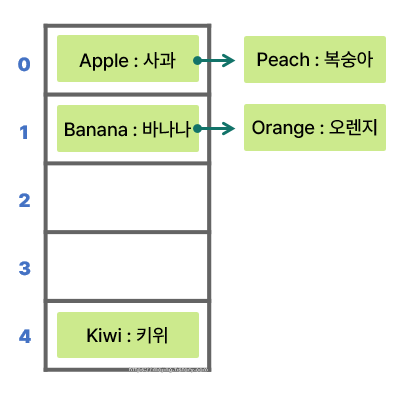
🧩 <해시 테이블: 검색>
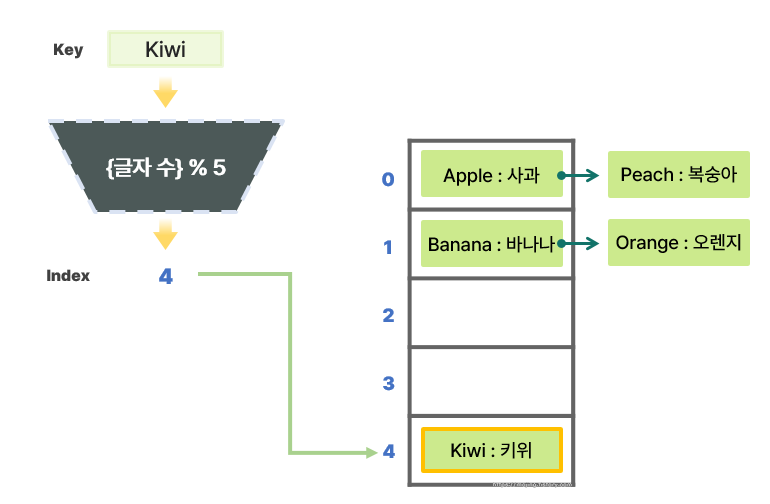
- `"Kiwi"`의 뜻을 알고 싶다고 가정하면, 먼저 `"Kiwi"`가 어디에 저장되어 있는지 알기 위해 해시 값을 구해야 한다.
- `"Kiwi"`의 해시 값은 4 % 5의 결과인 4이므로 해당 인덱스에 저장된 데이터의 키가 `"Kiwi"`인지 검사한다.
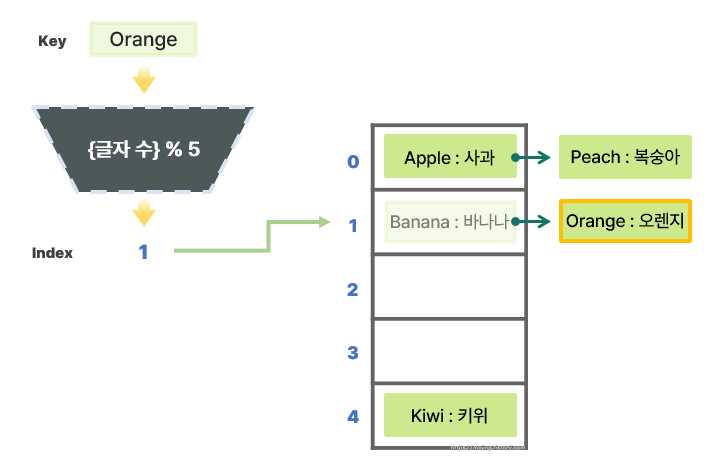
- 다음으로 `"Orange"`의 뜻을 알고 싶다고 가정하면, 1번 인덱스에서 `"Banana"`와 가장 먼저 마주치게 될 것이다.
- 이때는 해당 인덱스에서 선형 탐색을 진행하게 된다. 따라서 `"Banana"`를 시작으로, 키가 `"Orange"`인 데이터를 찾을 때까지 연결된 리스트를 모두 탐색한다.
- 1번 인덱스의 두 번째 리스트에서 `"Orange"`의 뜻(값, Value)인 `"오렌지"`를 추출할 수 있다.
📌 해시 테이블의 장점
- 검색 속도가 빠르다.
- ⏱ 평균 시간 복잡도가 $\mathbf{O(1)}$로, 매우 빠른 검색이 가능하다.
- ❗ 충돌이 많을 경우, 최악의 시간 복잡도인 $\mathbf{O(n)}$까지 증가할 수 있다.
- 해시 테이블은 키를 기준으로 데이터를 저장하므로, 중복 검사 과정이 매우 빠르고 간단하다.
- 유연한 키-값 저장과 동적으로 크기 조절이 가능하다.
- 다양한 타입의 데이터를 저장할 수 있다.
- 연결 리스트를 사용하므로, 저장할 데이터 수가 정해져 있지 않더라도 유연한 대응이 가능하다.
📌 해시 테이블의 단점
- 충돌(Collision) 발생
- 해시 함수가 동일한 해시 값을 생성하거나, 배열의 크기가 너무 작으면 충돌이 많아지고, 선형 탐색 빈도가 높아진다.
- 따라서 적절한 충돌 해결 기법이 필요하다.
- 메모리 사용량이 많다.
- 배열 기반이므로 사용되지 않는 공간이 생길 가능성이 높다.
- 데이터 삽입 순서를 보장하지 않는다.
- 해시 함수를 신중하게 설계해야 한다.
- 해시 함수가 데이터를 균등하게 분배하도록 해야 한다. 그렇지 않으면 특정 주소에 데이터가 몰려 성능이 저하될 수 있다.
📌 해시 테이블의 사용
주로 검색을 자주 하고 삽입/삭제도 빈번한 경우 유용하다.
- C#의 `Dictionary`, C++의 `unordered_map` 구현
- 데이터베이스 인덱싱
- 일부 데이터베이스 관리 시스템은 데이터를 빠르게 검색하기 위해, 해시 테이블 기반 인덱스(Hash Index)를 사용한다.
- ` SELECT * FROM Users WHERE user_id = 1002;` 의 WHERE절에서 `user_id`를 검색하는 경우, 해시 인덱스는 $O(1)$의 속도로 데이터의 저장 주소를 찾아낸다.
- 캐싱(Cache) 시스템
'💾 Computer Science > Algorithm' 카테고리의 다른 글
| [Data Structure] 자료구조 - 큐(Queue), 원형 큐, 우선순위 큐, 데크 (0) | 2024.11.04 |
|---|---|
| [Algorithm] Longest Common Subsequence(LCS) 알고리즘 : 두 문자열 간 최장 공통 부분 수열 찾기 (1) | 2024.10.22 |
| [Algorithm] 선형 에라토스테네스의 체(선형 체, Linear Sieve) : O(n)으로 소수 구하기! (1) | 2024.10.16 |
🗨 개인적인 공부 기록용으로 정리한 내용입니다. 잘못된 내용에 대한 피드백은 언제나 감사합니다 :)
⭐ 해시 테이블은 키(Key)를 해시 함수를 통해 해시 값으로 변환하고, 이를 인덱스로 사용하여 데이터를 저장하는 자료구조이다.
📌 해시 테이블의 정의
해시 테이블은 키(Key)를 특정 연산(해시 함수, Hash Function)을 통해 해시 값(Hash Value)으로 변환하고, 이를 인덱스로 사용하여 데이터를 저장하는 키-값(Key-Value) 매핑 자료구조이다.
일반적으로 해시 맵(Hash Map)이라고도 하며, 빠른 검색, 삽입, 삭제가 가능한 점이 특징이다.
키-값 구조는 "사전(Dictionary)"으로 예를 들 수 있다.
사전(Dictionary)은 단어(키, Key)와 뜻(값, Value)을 매핑하는 구조이다. 예를 들어 "Apple"이라는 단어로 검색을 한다면 "사과"라는 뜻을 얻을 수 있다.
해시 테이블은 이러한 사전의 개념을 프로그래밍에서 그대로 구현한 자료구조이다.
🔖 해시 테이블의 동작 원리
❓ "배열에 저장하면 되는데 왜 해시 테이블을 쓰는가?"
해시 테이블은 배열과는 비교할 수 없는 똑똑하고 빠른 검색 속도가 가장 큰 특징이다.
(똑똑한 방법이라고 한 이유는 컴퓨터에서는 모든 정보가 "수"로 이루어진 점을 이용해 수학적이고 효율적으로 데이터를 관리하는 방법이기 때문이다.)
예를 들어 물건을 정리할 때, 모든 물건을 한 공간에 모아둘 수도 있지만, 구역을 나눠서 "이건 A구역, 저건 B구역.." 이런 식으로 정리를 하면 나중에 찾을 때 해당 구역만 탐색을 하면 되기 때문에 효율적이다.
위의 정리 방법 중 전자는 배열, 후자는 해시 테이블의 데이터 저장 방식과 유사하다.
자세한 동작 원리는 다음과 같다.
배열과 해시테이블의 데이터 저장 및 검색 과정을 비교하였다.
- 아래의
키-값 구조의 데이터를 저장하려고 한다.

🧩 <배열: 저장>
배열의 경우, 고정된 크기의 공간에 차례대로 저장된다.

🧩 <배열: 검색>
- 여기서
"Orange"의 뜻을 알고 싶다고 가정하면, 배열의 0번 인덱스부터선형 탐색을 한다. - 2번 인덱스에 저장된 키(Key)가
"Orange"와 일치하므로 값(Value)을 불러온다.
⏱ 선형 탐색은 $\mathbf{O(n)}$ 의 시간 복잡도를 가지므로 데이터가 많을수록 찾는 시간도 오래 걸린다.

🧩 <해시 테이블: 저장>
해시 테이블은 키를 해시 함수를 이용하여 인덱스로 변환하고, 해당 인덱스에 키-값 데이터를 저장한다.
키와 해시 함수로 실제 데이터를 저장할 주소를 반환받는 것이다.
❓ 해시 함수 (Hash Function)
해시 함수란? 주어진 데이터를 고정 길이의 불규칙한 숫자로 변환하는 함수를 가리킨다.
해시 함수의 대표적인 알고리즘으로 SHA가 있다. 🔗 SHA
아래에서 사용하는 해시 함수는 모듈로 연산(나머지 연산, mod)을 이용하였다. (글자 수 % 배열 크기)
이처럼 나머지 연산자(mod)를 사용해 키를 해시 테이블의 크기로 나눈 나머지를 해시 주소로 사용하는 방법을 제산함수라고 한다.
- 먼저 키(Key)인
"Apple"을 해시 함수를 이용해 해시 값을 추출한다. "Apple"의 글자 수는 5이므로 해시 값으로 0이 나온다. 이 0을 인덱스로 이용하여 키-값 데이터를 저장한다.

- 키(Key)
"Banana"는 해시 함수를 이용해 변환하면 6 % 5 = 1이므로, 1번 인덱스에 데이터를 저장하게 된다.

- 키(Key)
"Orange"는 해시 함수를 이용해 변환하면 6 % 5 = 1이므로, 1번 인덱스에 데이터를 저장하게 된다. - ❗ 그런데 이미 1번 인덱스에는
"Banana"의 데이터가 저장되어 있다. 이렇게 서로 다른 키(Key)가 해시 함수에 의해 저장 위치가 겹치는 것을 충돌(Collision)이라 한다.

- 겹친 저장위치에 저장을 시도하면 오버플로우(Overflow)가 발생하므로, 충돌 문제 해결 방법이 필요하다.
- 대표적인 충돌 해결 방법에는 두 가지가 있다.
체이닝(Chaining): 같은 해시 값을 가지는 데이터들을 연결 리스트(Linked List) 또는 트리(Tree)를 사용하여 저장하는 방식.오픈 어드레싱(Open Addressing): 충돌이 발생하면 다른 빈 공간을 찾아 데이터를 저장하는 방식.
- 이 중에 연결 리스트를 사용하는 체이닝 기법을 이용하면 아래와 같다.

- 나머지 데이터들을 저장하면 아래와 같다.

🧩 <해시 테이블: 검색>
"Kiwi"의 뜻을 알고 싶다고 가정하면, 먼저"Kiwi"가 어디에 저장되어 있는지 알기 위해 해시 값을 구해야 한다."Kiwi"의 해시 값은 4 % 5의 결과인 4이므로 해당 인덱스에 저장된 데이터의 키가"Kiwi"인지 검사한다.

- 다음으로
"Orange"의 뜻을 알고 싶다고 가정하면, 1번 인덱스에서"Banana"와 가장 먼저 마주치게 될 것이다. - 이때는 해당 인덱스에서 선형 탐색을 진행하게 된다. 따라서
"Banana"를 시작으로, 키가"Orange"인 데이터를 찾을 때까지 연결된 리스트를 모두 탐색한다. - 1번 인덱스의 두 번째 리스트에서
"Orange"의 뜻(값, Value)인"오렌지"를 추출할 수 있다.

📌 해시 테이블의 장점
- 검색 속도가 빠르다.
- ⏱ 평균 시간 복잡도가 $\mathbf{O(1)}$로, 매우 빠른 검색이 가능하다.
- ❗ 충돌이 많을 경우, 최악의 시간 복잡도인 $\mathbf{O(n)}$까지 증가할 수 있다.
- 해시 테이블은 키를 기준으로 데이터를 저장하므로, 중복 검사 과정이 매우 빠르고 간단하다.
- 유연한 키-값 저장과 동적으로 크기 조절이 가능하다.
- 다양한 타입의 데이터를 저장할 수 있다.
- 연결 리스트를 사용하므로, 저장할 데이터 수가 정해져 있지 않더라도 유연한 대응이 가능하다.
📌 해시 테이블의 단점
- 충돌(Collision) 발생
- 해시 함수가 동일한 해시 값을 생성하거나, 배열의 크기가 너무 작으면 충돌이 많아지고, 선형 탐색 빈도가 높아진다.
- 따라서 적절한 충돌 해결 기법이 필요하다.
- 메모리 사용량이 많다.
- 배열 기반이므로 사용되지 않는 공간이 생길 가능성이 높다.
- 데이터 삽입 순서를 보장하지 않는다.
- 해시 함수를 신중하게 설계해야 한다.
- 해시 함수가 데이터를 균등하게 분배하도록 해야 한다. 그렇지 않으면 특정 주소에 데이터가 몰려 성능이 저하될 수 있다.
📌 해시 테이블의 사용
주로 검색을 자주 하고 삽입/삭제도 빈번한 경우 유용하다.
- C#의
Dictionary, C++의unordered_map구현 - 데이터베이스 인덱싱
- 일부 데이터베이스 관리 시스템은 데이터를 빠르게 검색하기 위해, 해시 테이블 기반 인덱스(Hash Index)를 사용한다.
SELECT * FROM Users WHERE user_id = 1002;의 WHERE절에서user_id를 검색하는 경우, 해시 인덱스는 $O(1)$의 속도로 데이터의 저장 주소를 찾아낸다.
- 캐싱(Cache) 시스템
'💾 Computer Science > Algorithm' 카테고리의 다른 글
| [Data Structure] 자료구조 - 큐(Queue), 원형 큐, 우선순위 큐, 데크 (0) | 2024.11.04 |
|---|---|
| [Algorithm] Longest Common Subsequence(LCS) 알고리즘 : 두 문자열 간 최장 공통 부분 수열 찾기 (1) | 2024.10.22 |
| [Algorithm] 선형 에라토스테네스의 체(선형 체, Linear Sieve) : O(n)으로 소수 구하기! (1) | 2024.10.16 |
